While it can be easy to identify the position of a highlight, because of its value contrast to the surrounding form, it can be difficult to determine the position of the highest form light on a form.
Even though high form lights may not appear to be as obvious as highlights, one can reverse engineer from the light source's position in relation to a viewer to determine the position of a high form light in relation to a highlight.¹ To do this, something must be known about highlights and high form lights.
Highlights on a form are visible halfway between the angle of light projected by a light source in single path known as a light ray, and the angle of that light ray's reflection into a viewer's eye. High form lights are the point on a form that is most parallel to the angle of a light source. Note, in this post I will use the term highlight to refer to the concentrated area of specular reflection on a form that is seen by a viewer.
Description of Highlights
Highlights are caused by specular reflection and highlights are essentially made up of specular reflections. Specular reflection is the mirror-like reflection of light on a smooth glossy surface where the angle of incoming light projected in a single direction from the light source, the angle of incidence, is reflected at the same angle into a viewer's eye, the angle of reflection. Therefore, the angle of incidence equals the angle of reflection.
An example of a specular reflection on a sphere.
Many specular reflections cause the large highlight area on the sphere.
A useful analogy that I thought of to help visualize the effect of specular reflection is to imagine hitting a tennis ball on the ground.
The illustration above shows how the angle that the tennis ball is hit at is the same angle that it is reflected at, similar to how in specular reflection the angle of incidence is always the same angle as the angle of reflection. This principle holds true no matter what angle the tennis ball is hit at. If the tennis balls in this analogy were photons of light and the path that each tennis ball followed was a light ray then the specular reflection would occur where the light ray hits the surface of the ground, the halfway point between the angle of incidence and the angle of reflection.
Specular reflection is only visible at the halfway point between the angle of incidence and the angle of reflection into a viewer's eye. A useful analogy that I thought of to help visualize this effect is to imagine you are standing on a tennis court, across from a giant tennis ball machine. The tennis ball machine projects millions of tennis balls at one moment. But, you will only be hit by the tennis balls that are in your line of sight.
The point where the tennis balls in your line of sight hit the ground would be the halfway point between the angle of incidence and the angle of reflection into your eye. If the tennis ball machine in this analogy was a light source, the tennis balls were photons of light, the path that each tennis ball followed was a light ray and the ground was the surface of a form then the specular reflection would be seen at the point where the tennis balls in your line of sight hit the ground (the halfway point between the angle of incidence and the angle of reflection into your eye). The blue circles on the ground in the above illustration show the area where the specular reflection would be seen for light ray A and light ray B. The area between where both of these light rays hit the ground is so close that the blue circles are touching. The grouping of the two blue areas where specular reflection would be seen by the viewer is the same as how specular reflections group together to show a brighter and larger highlight area. The viewer in this highlight analogy would be hit by different tennis balls in their line of sight depending on where they were located on the tennis court and the area where those tennis balls hit the ground, the area where a highlight would be seen, would change as the viewer moved.
The same principles that apply to the tennis ball analogy are present while viewing a highlight in real life.
Viewing Highlights
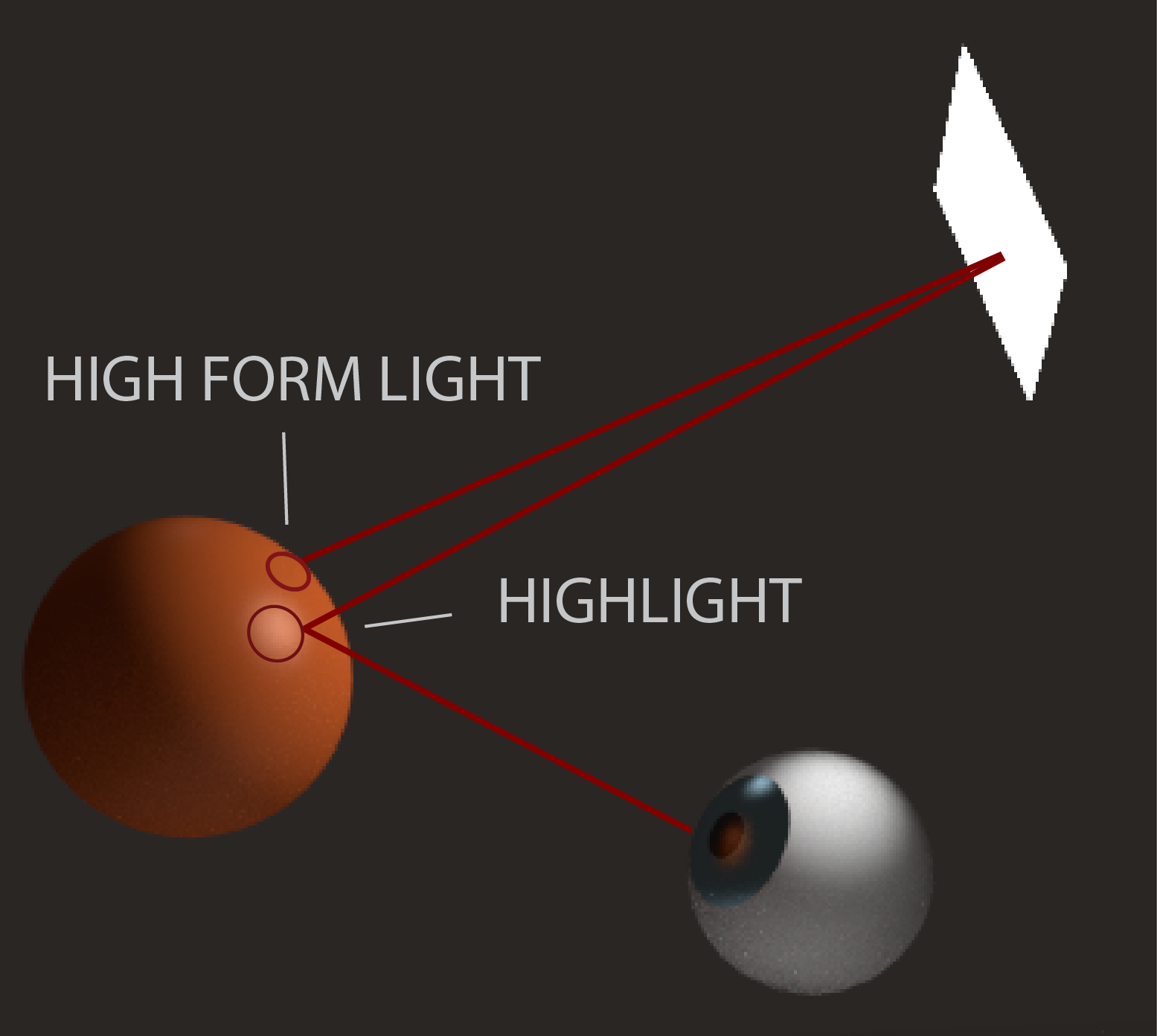
Because highlights are visible when the angle of incidence equals its angle of reflection into a viewer's eye, the highlight shares the same relationship to the high form light as the relationship of a viewer's position to a light source.¹
By knowing one's position in relation to the center of a light source, one can identify where the high form light is in relation to the center of a highlight.¹ The diagram above shows how the position of the viewer in relation to the light correlates to the position of the high form light in relation to a highlight. For example, the light is very far to the right of viewer A, so the high form light, outlined in red, is very far to the right of the highlight that viewer A sees. Also, the light is closer to the left of viewer B, so the high form light is closer to the left of the highlight that viewer B sees.
Additionally, the location of the high form light in relation to a highlight changes vertically with a viewer's relation to a light source.¹ In the diagram above, the light is above and to the right of the viewer, so the high form light, outlined in red, is above and to the right of the highlight. It should be noted that although the relationship of the highlight to the high form light generally correlates to the relation of the viewer to the light source, that distance can not be pinned down to a measurable distance. For example, just because a viewer is 5 feet to the left of the light does not mean that the highlight is 5 feet to the left of the high form light. But the distance of the highlight in relation to the high form light will generally correlate to the distance of the viewer in relation to the light source.
Footnotes
¹ Jeremy Deck, personal communication, 2013.